Exercises
Here you can find exercises in the many uses of the Scandinavian Beer Calculator.
This page is available as Adobe PDF: 17 exercises in beer Calculation (2006)
Abbreviations:
| hl |
= |
Beer volume |
In hectoliter, 100 liter |
| OE%P |
= |
Extract in Original Wort |
In % Plato, g/100 g |
| ER% |
= |
Real Extract |
In %, g/100 g |
| EA% |
= |
Apparent Extract |
In %, g/100 g |
| A%mas |
= |
Alcohol content by mass |
In %, g/100 g |
| A%vol |
= |
Alcohol content by volume |
In %, ml/100 ml |
| RDF% |
= |
Real Degree of Fermentation |
In %, g/100 g |
| ADF% |
= |
Apparent Degree of Fermentation |
In %, g/100 g |
| SGA |
= |
Specific Gravity of distillate |
|
| SGE |
= |
Specific Gravity of Reminiscence |
|
| SGBeer |
= |
Specific Gravity of Beer |
|
| NUTV |
= |
Nutritive Value of Beer |
In kJoule/100 ml |
| CALV |
= |
Calorific Value of Beer |
In kCal/100 ml |
| FRZP° |
= |
Freezing Point of Beer |
In degree Celsius |
| TMXD° |
= |
Temperature of Max. Density |
In degree Celsius |
| BOD5 |
= |
Biological Oxygen Demand |
In mg/liter |
| OEkg |
= |
Kg of Original Extract |
In kg |
Beer Calculations made by The Scandinavian Beer Calculator
First: Adjust to "View / Full screen" and activate "Decimals" to make the screen easy to see.
Exercise 1: Calculate RDF% ASBC and RDF%Classic, when OE%P = 10 and ER% = 5
-
Enter OE%P=10 and ER%=5
-
Calculate and read: RDF% ASBC= 51.3 and RDF% Classic = 50
Exercise 2: Calculate ADF%, when OE%P = 10 and EA% = 5
-
Enter OE% P= 10, and EA% = 5
-
Calculate and read: ADF% =50
Exercise 3: Find the composition of beer which has SGBeer = 1 and OE%P = 12
-
Enter: OE%P = 12 and SGBeer = 1
-
Calculate and read: RDF% = 81.8 and ADF% = 100.0
Exercise 4: Find a composition of beer which has SGBeer = 1 and OE%P = 20
-
Enter: OE%P = 20 and SGBeer = 1
-
Calculate and Read: RDF% = 82.4 and ADF% = 100.0
-
When SGBeer =1 then RDF% will always be near 82!
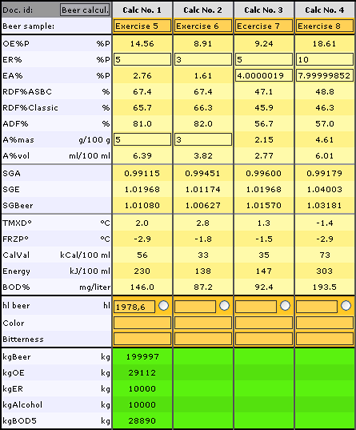
Exercise 5: How many hl of beer (ER% = A%mas=5.00) is required to contain 1,000 kg Alcohol?
-
Enter: A%mas = 5 and ER% = 5
-
Adjust hl to get Akg = 1,000
-
Read: hl=1978.6 and RDF%= 67.4
Exercise 6: Calculate RDF% ASBC for a beer having ER% = A%mas = 3, and compare with the above.
-
Enter: A%mas = 3 and ER% = 3
-
Read: RDF%ASBC = 67.4, which is the same as above
Exercise 7: Calculate the composition of beer, when ER% = 5 and EA% = 4.
How correct is the formula: ER%-EA% = 0.46 x A%mas?
-
Enter: ER% = 5
-
Read: A%mas = 2.1545 (which will justify ER% -EA% = 0.46 x A%mas)
-
For this beer the formula is good!
Exercise 8: Calculate the composition of beer, when ER% = 10 and A%mas = 8
How correct is the formula: ER%-EA% = 0.46 x A%mas?
-
Enter: ER% = 10 and EA% = 8
-
Read: A%mas =4.611% (which only will justify: ER% -EA% = 0.43 x A%mas)
-
This formula is not acceptable for strong beer.
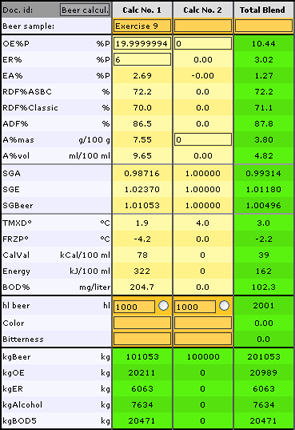
Exercise 9: Which values for OE%P and ER% will we get, when we mix 1,000 hl beer having OE%P=20.00 and ER%=6.00 with 1000 hl D-water?
-
Enter in the first column: ER%=6.00 OE%P=20.00 hl=1000
-
and in the second column : OE%P = 0 A%mas = 0 hl=1000 (Water!)
-
Read for Total Blend: OE%P=10.44 and ER% = 3.02
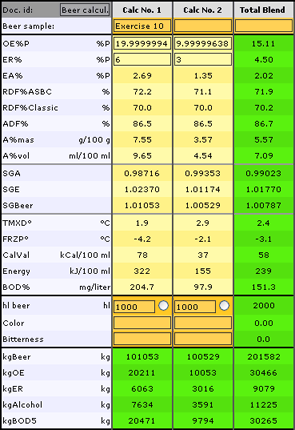
Exercise 10: Which values for OE%P will we get, when we mix 1,000 hl beer having OE%P=20.00 and ER%=6.00 with 1,000 hl beer having OE%P=10.00 and ER%=3.00?
-
Enter in the first column: ER% = 6.00 OE%P=20.00 hl=1000
-
and in the second column : ER% = 3.00 OE%P=10.00 hl=1000
-
Read for Total Blend: OE%P=15.11
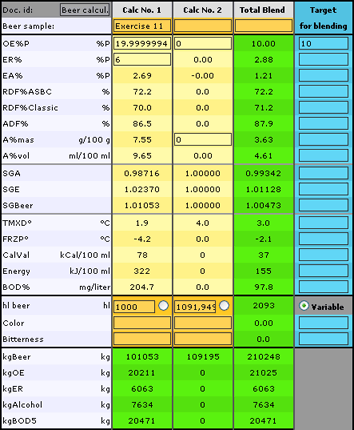
Exercise 11: How much D-water shall we mix into 1,000 hl HGB-beer having OE%P=20.00 and ER% = 6.00 to get OE%P=10.00 in the blend? Will the water change RDF%Classic or RDF% ASBC?
-
Enter in the first column: ER% = 6.00 OE%P=20 hl=1000
-
and in the second column : OE%P = 0 A%mas = 0 (Water)
-
Enter OE%P=10.00 as “Target for blending”.
-
Calculate and read: hl=1,092 (water) and RDF%ASBC = 72.2 (unchanged).
-
Read the result of dilution for RDF% Classic. It is increased from 70.0 to 71.2%!
Only RDF%ASBC remains unchanged at dilution!
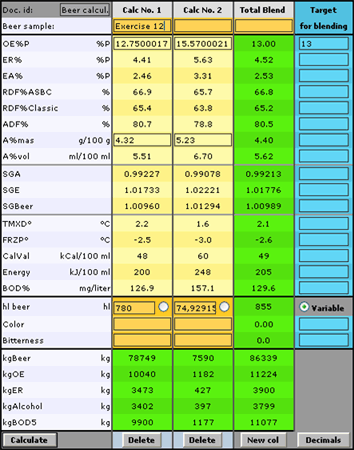
Exercise 12: A beer tank contains 780 hl beer (Brand A) having OE%P = 12.75 and A%mas = 4.32
The strength should be OE%P = 13.00
How much of Brand B (OE%P = 15.67 and A%mas = 5.23) shall we mix into brand A?
-
Enter in the first column: OE%P = 12.75 A%mas = 4.32 hl=780
-
and in the second column : OE%P = 15.67 A%mas = 5.23
-
Enter as "Target for blending": QE%P = 13
-
Indicate that the volume of Brand B in the second box is variable (Click in the ring)
-
Calculate and read: hl =75 (Brand B in the second box)
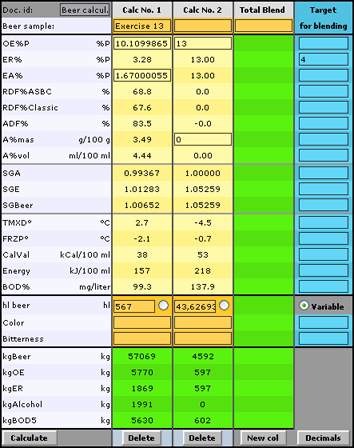
Exercise 13: To a tank of 567 hl beer (OE%P=10.11 and EA% = 1.67) wort (OE%P = 13.00 and A%mas = 0) shall be added to give ER%=4.00
Calculate how many hl cold wort will be required.
-
Enter in the first column: OE%P=10.11 EA% = 1.67 hl=567
-
and in the second column : A%mas = 0 OE%P=13.00
-
Enter as "Target for blending": ER = 4
-
Indicate that the volume of wort in the second box is variable (Enter a dot in the ring)
-
Calculate and read: hl = 44 (of wort in the second box)
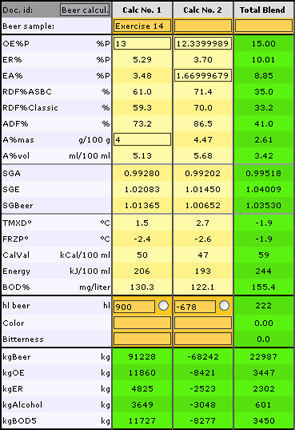
Exercise 14: To 678 hl beer (OE%P=12.34 and EA% = 1.67) shall we add 222 hl beer to fill up the tank.
Which composition shall this beer have to make OE%P = 13 and A%mas = 4 in the final blend?
We make this calculation by subtraction of the first beer from the final blend.
-
Enter the final blend in the first column: OE%P =13 A%mas = 4 hl=678+222 = 900
-
And the original beer in the second column: OE%P = 12.34 EA% = 1.67 hl = -678
Calculate and read the composition of the added beer as "Total blend":
-
OE%P = 15.00 and RDF%ASBC = only 35! (This is not a fully fermented beer!).
Note that The Scandinavian Beer Calculator will accept negative volumes!
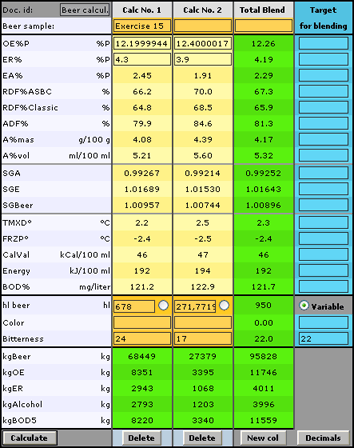
Exercise 15:
Brand A has a composition of OE%P = 12.2 ER% = 4.3 and Bitterness = 18
How much of Brand B OE%P = 12.4 ER% = 3.9 and Bitterness = 24
shall we mix into 567 hl of Brand A to make Bitterness = 20.5 in the blend?
-
Enter in the first column: OE%P=12.2 ER% = 4 Bitterness = 24 hl = 678
-
and in the second column : OE%P=12 A%mas = 4 Bitterness = 17
-
Enter as "Target for blending": Bitterness = 22
-
Indicate that the volume of Brand B in the second box is variable (Enter a dot in the ring)
-
Calculate and read: hl = 272 (of Brand B in the second column)
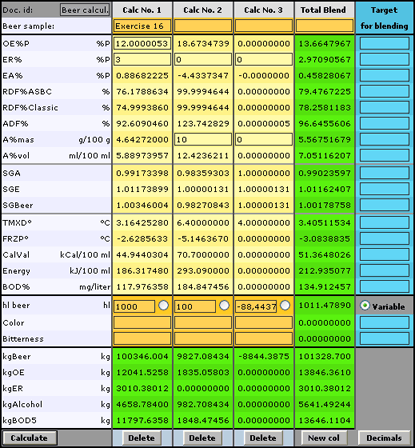
Exercise 16:
Calculate the density of alcohol, when dissolved in beer.
-
Enter in the first column figures for a normal beer: OE%P = 12.00 ER%=3.00 hl=1000
-
Enter in second column figures for an alcohol solution: A%mas = 10.00 ER%=0 hl=100
-
Subtract in the third column the mass of water contained in the alcohol solution (9827.084 – 982.708 = 8844.37 kg = 88.4437 hl):
-
Enter in the third column: A%mas = 1 ER% = 0 hl = -88.4437
-
Read: The Increase in volume = 11.4789 hl (Total blend – beer in first column)
-
Read: Mass of Alcohol added in the second column = 982.708kg
-
Density: 982.708/1147.89 = 0.87 g/ml
-
(The table value for the density of pure alcohol is 0.781 g/ml. Alcohol in solution changes the molecule structure of the water in the beer and makes it more dense.)
Exercise 17:
Check the quality of interpolation in the applied Alcohol Table.
The Scandinavian Beer Calculator calculates SGA from A%mas by looking up and interpolating the value in a special version of the "OIML-EBC Table".
A section of this table is as follows:
| A%mas: |
5.67 |
5.68 |
5.69 |
5.70 |
5.71 |
| SGA: |
0.99007233 |
0.99005643 |
0.99004054 |
0.99002467 |
0.99000880 |
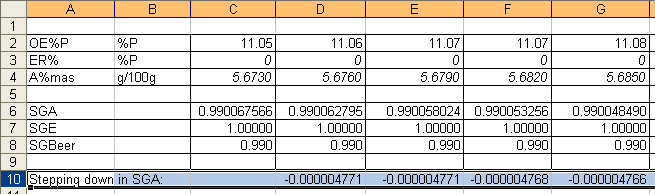
The table has only 2 decimals for A%mas. The interpolation should do up for further decimals.
To check the quality of this interpolation we will enter ER%mas = 0 and
the following series of A%mas values stepping up constantly with 0.003:
5.673 – 5.676 – 5.679 – 5.682 – 5.685
The figures on the screen are presented in an Excel spreadsheet, when "Export to Excel" is chosen in the Main menu. The less interesting part of the spread sheet is eliminated, and the stepping-down values for SGA are calculated:
As seen above, fairly uniform steps for SGA have been calculated. This indicates a satisfactory quality of interpolation.
-End of 17 Exercises- |